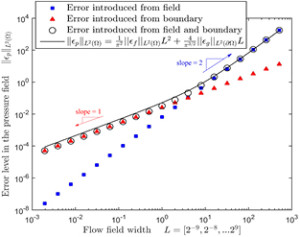
We are pleased to announce the publication of a paper in Measurement Science and Technology entitled “Error propagation dynamics of PIV-based pressure field calculations: How well does the pressure Poisson solver perform inherently?” In the article we use mathematics to explain why and how the Poisson equation increases errors from PIV data. The abstract is below and the full article can be found here.

Abstract: Obtaining pressure field data from particle image velocimetry (PIV) is an attractive technique in fluid dynamics due to its noninvasive nature. The application of this technique generally involves integrating the pressure gradient or solving the pressure Poisson equation using a velocity field measured with PIV. However, very little research has been done to investigate the dynamics of error propagation from PIV-based velocity measurements to the pressure field calculation. Rather than measure the error through experiment, we investigate the dynamics of the error propagation by examining the Poisson equation directly. We analytically quantify the error bound in the pressure field, and are able to illustrate the mathematical roots of why and how the Poisson equation based pressure calculation propagates error from the PIV data. The results show that the error depends on the shape and type of boundary conditions, the dimensions of the flow domain, and the flow type.