At APS 2016 in Portland, Oregon we were happy to submit several talks, posters, and videos. The titles and short abstracts for each one are listed below. We had an amazing time at APS and are very proud of the incredible work our students accomplished last semester.

Bird beaks bear the brunt of bashing impact

Seabirds can dive from 30 meters reaching speeds of 24 meters per second as they impact the water reaching depths of 9 meters due to their momentum, and a further 25 meters by active flapping. It is thought that their geometry, particularly the beak, allows them to endure relatively high impact forces that could kill non-diving birds. Acceleration data of simplified models of diving birds agree with simulated data for one species, however, no reliable experimental data with real bird geometries exist for comparison. We experimentally measured the impact accelerations of twelve 3D printed models of diving birds (seven surface diving and five plunge diving) during water-entry at different impact velocities using accelerometers.

Stable, streamlined and helical cavity formation by the impact of Leidenfrost spheres

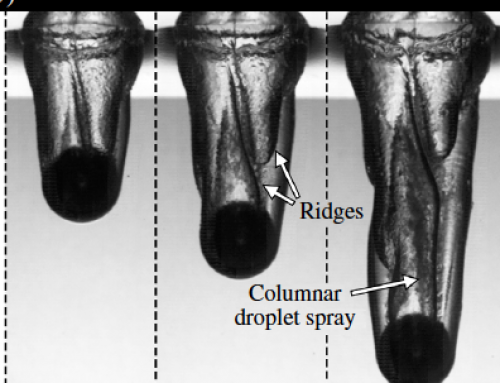
This work reports results from an experimental study on the formation of stable-streamlined and helical cavity wakes following the free-surface impact of Leidenfrost spheres. The Leidenfrost effect encapsulates the sphere by a vapor layer to prevent any physical contact with the surrounding liquid. This phenomenon is essential for the pacification of acoustic rippling along the cavity interface to result in a stable-streamlined cavity wake. Such a streamlined configuration experiences drag coefficients an order of magnitude lower than those acting on room temperature spheres. A striking observation is the formation of helical cavities which occur for impact Reynolds numbers Re0≥1.4×105 and are characterized by multiple interfacial ridges, stemming from and rotating synchronously about an evident contact line around the sphere equator. This helical configuration has 40−55% smaller overall force coefficients than those obtained in the formation of stable cavity wakes.

Make water entry great again!

Upon free surface impact, silicone rubber spheres deform significantly and begin to vibrate producing unique nested cavities. We show that sphere deformation and cavity formation can be characterized by material shear modulus, density and impact velocity. Additionally, material vibration scales with sphere diameter and material wave speed. Applying a modified diameter, which reflects deformation, effectively collapses experimental pinch-off data with Froude number. A scaling argument shows that a deformable sphere loses energy proportional to the vibrational period of the sphere in the first stages of impact. The effective force coefficient of a deformable sphere through impact is nearly identical to a rigid sphere with the same solid-liquid density ratio. The scaling predicts how the cavity and projectile dynamics of a deformable sphere differs from a rigid counterpart.

Bubble baths: just splashing around?

Soap Bubbles on the water surface would seem to be an intuitive means for splash suppression, but their presence appears to be a double edged sword. We present on the water entry of hydrophilic spheres where the liquid surface is augmented by the presence of a bubble layer, similar to a bubble bath. While the presence of a bubble layer can diminish splashing upon impact at low Weber numbers, it also induces cavity formation at speeds below the critical velocity. The formation of a cavity generally results in larger Worthington jets and thus, larger amounts of ejected liquid. Bubble layers induce cavity formation by wetting the sphere prior to liquid impact, causing them to form cavities similar to those created by hydrophobic spheres. Droplets present on a pre-wetted sphere disrupt the flow of the advancing liquid during entry, pushing it away from the impacting body to form an entrained air cavity. This phenomena was noted by Worthington with pre-wetted stone marbles, and suggests that the application of a bubble layer is generally ineffective as a means of splash suppression.

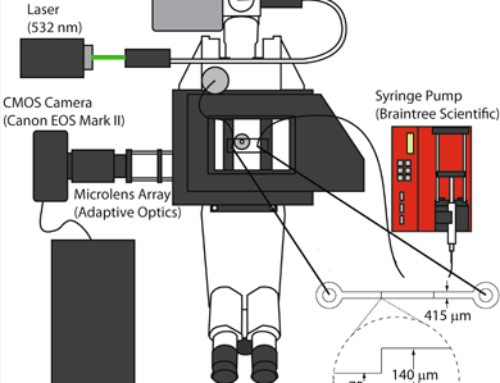
Droplet impact on a needle

A droplet impinging a hydrophobic surface (low {\it We}) spreads to a maximum diameter before retracting to the center of impact and sometimes lifting off. If the impact surface is augmented by a small ridge, the droplet will often split at this surface feature upon spreading resulting in a shorter time to lift off [Bird et. al., Reducing the contact time of a bouncing drop. {\it Nature}, {\bf 503}, 2013]. We investigate how a singular feature (needle point) generates a similar reduction in droplet contact time. Droplets of diameter (< 2 mm) were controlled to impact varying needles at various impact velocities ({\it We} range: 16 – 256). While it was initially supposed that splitting the droplet into more pieces would further decrease contact time, this was not observed. Rather, the spreading event at the center of the droplet has a greater effect on contact time.

The water entry of water

Though water entry has been studied for over a century, there has been a disconnect between solid object water entry and research on liquid impacting on a liquid pool. In addition, few have studied multiple objects impacting a liquid bath sequentially. We show that the impact of multi-droplet streams and liquid jets on a liquid pool display similar behavior to solid body water entry. In particular, the cavities of both droplet streams and jets exhibit three types of cavity seal previously found for hydrophobic spheres at low Bond numbers. Additionally, low-frequency droplet streams create three novel cavity seal types, which can be predicted with a new non-dimensional frequency. The cavity depth for both droplet and jet impact is rationalized by an energy scaling analysis. Finally, we examine the similarities and differences in cavity dynamics for multi-droplet streams and continuous liquid jets.

Error Propagation dynamics of PIV-based pressure calculation 2: from Poisson equations to Kirchhoff plates

Little research has been done to investigate the dynamics of error propagation from PIV-based velocity measurements to the pressure calculation. Rather than measure experimental error, we analytically investigate error propagation by examining the properties of the Poisson equation directly. Our results provide two contributions to the PIV community. First, we quantify the error bound in the pressure field by illustrating the mathematical roots of why and how PIV-based pressure calculations propagate. Second, we design the “worst case error” for a pressure Poisson solver. In other words, we provide a systematic example where the relatively small errors in the experimental data can lead to maximum error in the corresponding pressure calculations. The 2D calculation of the worst case error surprisingly leads to the classic Kirchhoff plates problem, and connects the PIV-based pressure calculation, which is a typical fluid problem, to elastic dynamics. The results can be used for optimizing experimental error minimization by avoiding worst case scenarios. More importantly, they can be used to design synthetic velocity error for future PIV-pressure challenges, which can be the hardest test case in the examinations.